机密计算: 可信与国密算法

可信根、可信链以及国密算法。

机密计算

可信认证

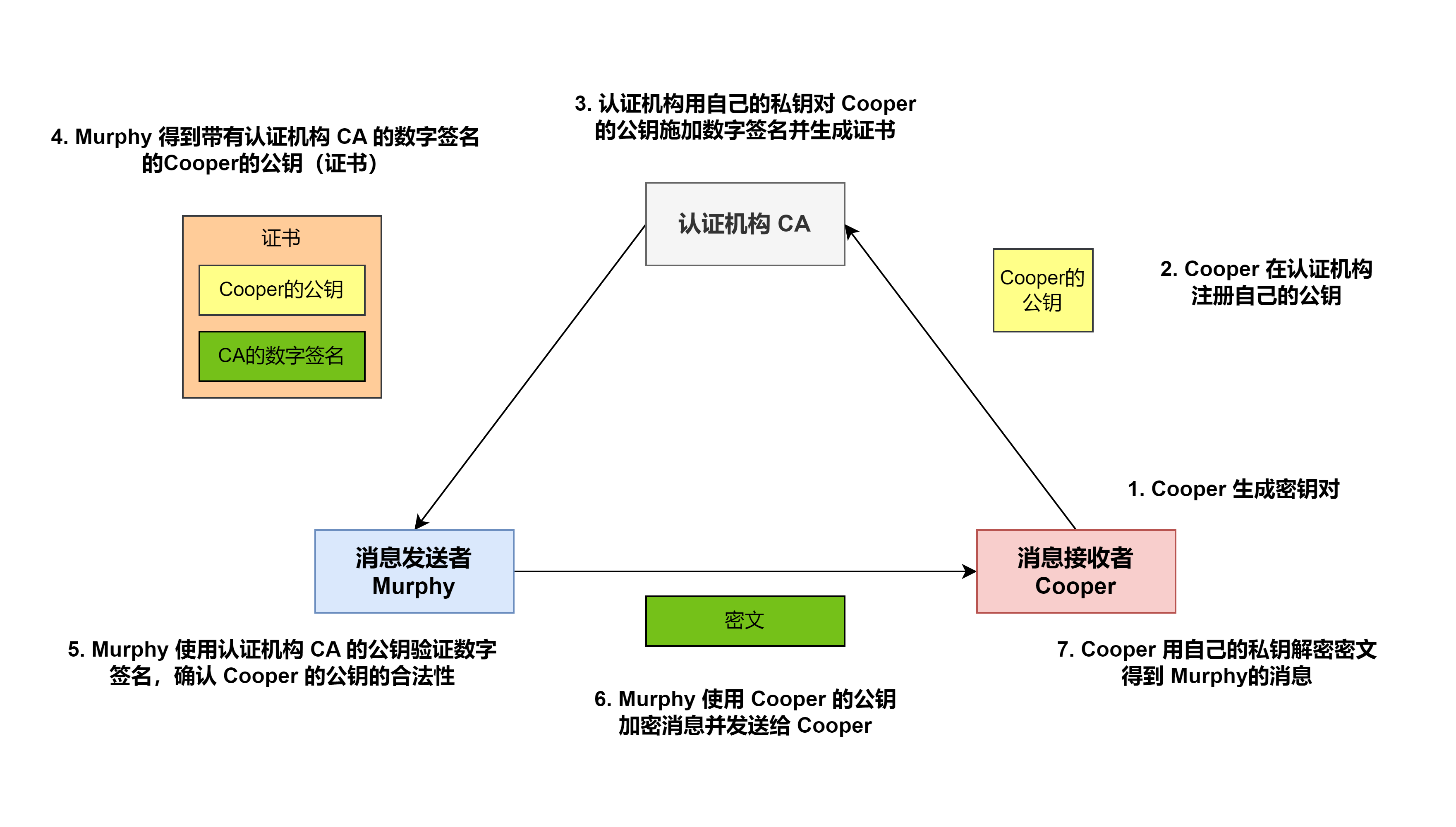
如何拿到合法的公钥：

  • 公钥证书：里面含有名字、组织、邮箱地址等基本信息，以及属于此人的公钥，由认证机构 (Certification Authority, Certifying Authority, CA) 施加数字签名
  • 认证机构：由国际性组织和政府所设立的组织，也有通过提供认证服务来盈利的一般企业，此外个人也可以成立认证机构

获取合法的公钥

可信根

  • 可信根的定义：如果信息系统中的可信机制是完整的，则沿着这个支撑关系回溯，最终会得到一个既具备安全功能又具备可信功能，而且不需要其他机制提供安全支撑的底层机制，这就是系统的可信根。
  • 可信根的基本属性：具备密码服务功能、具备对系统启动的度量能力、可以控制系统启动过程、先于系统其它部分启动
  • 可信根的基本组成：由具备密码服务功能的可信平台模块、以及系统中的度量代码段组成；可信平台模块拥有权限保护机制，需要更高的权限才可以访问到其片内的资源，例如只有安全处理器才可以访问到芯片的密钥；度量代码放在ROM中，固化在可信平台模块内部，无法被攻击。

可信链的建立

如何由可信根出发建立信任链：

  • 信任建立的基础：身份信息的确认，代码完整性的度量
  • 身份信息的确认：基于安全处理芯片中的公钥密码模块，通过签名和验签来实现
  • 代码完整性的度量：基于安全处理芯片中的单向散列函数模块，生成固定长度的散列值；与预期的散列值进行比较，实现完整性度量

任何一步验签失败，都会使得系统无法启动。

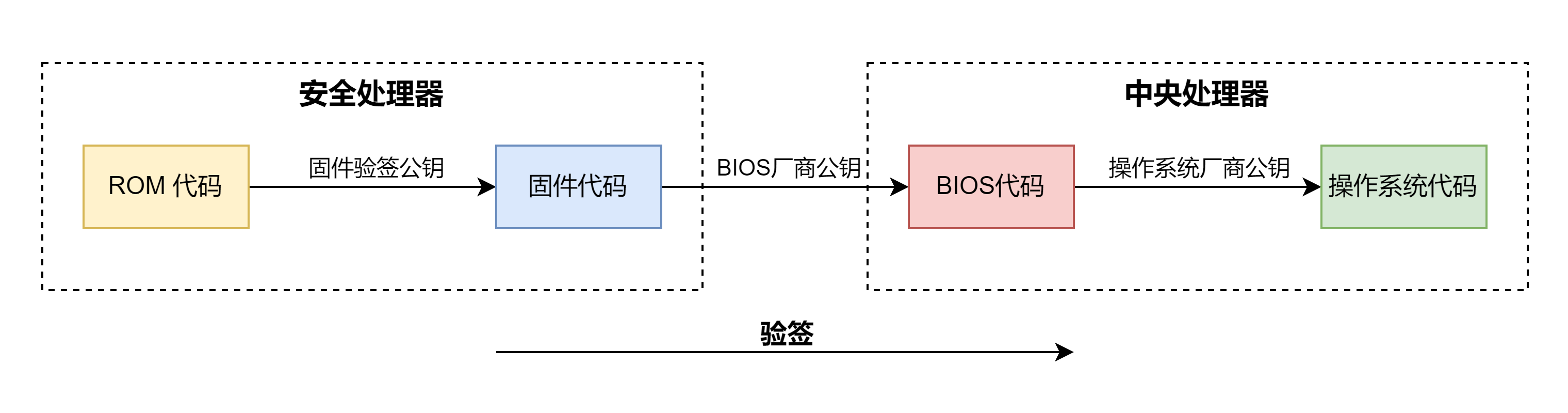
系统安全启动验签流程

片外固件结构

加密+签名（安全服务器中完成）：

  1. 在 Header 中填入加密参数（随机数），用于对固件 Body 进行加密；随机数会作为对称加密的初始化向量
  2. 对 Header + Body 计算摘要得到哈希值，然后进行签名操作
  3. 使用加密参数加密 Body
  4. 拼接 Header + Enc_Body + Signature

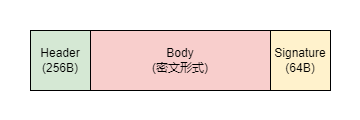
片外固件结构

解密+验签（Boot阶段由安全管理芯片完成）：

  1. 获得 Header 中的解密参数（随机数）
  2. 使用对称密码对 Body 进行解密；
  3. 对 Header + Dec_Body 计算摘要得到哈希值
  4. 对得到的哈希值进行验签

可信度量

静态度量

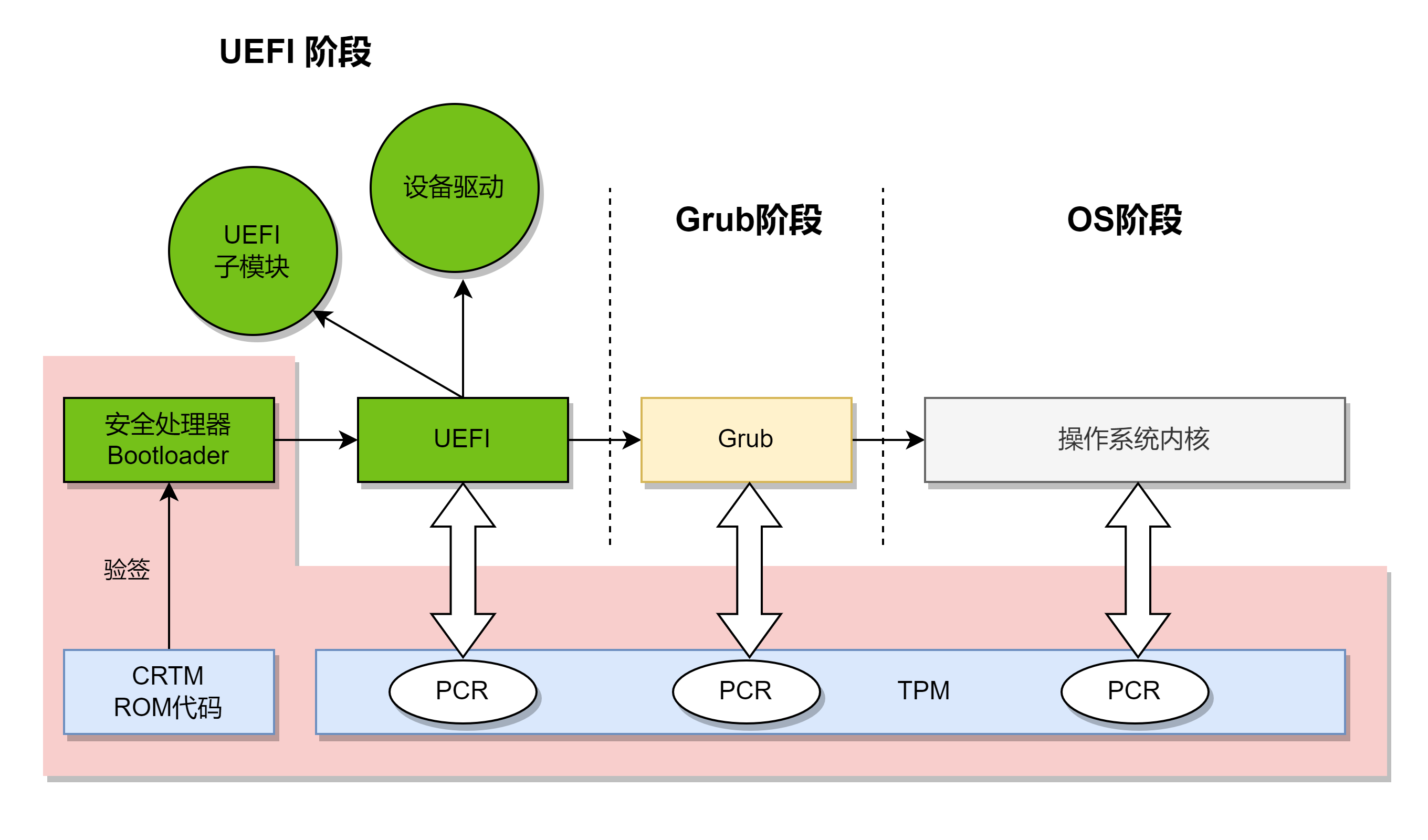
  • 逐级检查代码的完整性，度量的结果放在PCR(Platform Configurate Register)寄存器中；
  • 核心度量根 CRTM，就是 ROM 代码；
  • 服务器的 BIOS 都是 UEFI 模式；
  • 将预期值和 PCR 寄存器的值进行比对，确认代码的完整性。

动态度量：

  • TPCM 特性：TPM 只支持静态度量，国内 TPCM 标准可以支持动态度量
  • 动态度量：安全处理器对运行中的关键程序和数据进行度量监控，包括：
    • 中断向量表
    • 系统调用表
    • 内核模块
  • 度量报告：包含当前计算机的可信状态，同时对度量报告进行签名，无法伪造
  • Hy独有：TDM 轻量级动态度量，满足不同用户需求

Windows 运行 certmgr 命令可以查看证书：

查看证书

可信存储

  • 集成密码模块：在服务器的内存控制器中，集成了对称加解密引擎；
  • 对性能的影响：由于对称加解密的特点，对访存性能几乎没有影响；
  • 加密开关：在内存物理地址增加 C 位，作为加解密的开关，同时加解密以页为单位（4K页和2M页）；通过ASID来对应不同的虚拟机，实现应用层加密管理
  • 密钥管理：密钥由安全处理器管理、用户和操作承统均无法获得密钢：每个虚拟机对应一个不同的 ASID，内存加加解密的密钥由UMC内部逻辑产生.根据不同的ASID 和地址生成不同的密钥。

如何实现安全存储：

  • 数据加密：将数据进行加密后，放入磁盘
  • 访问授权：用户访问服务器需要提供授权码，授权正确才可以访问
  • 可信绑定：授权码和可信状态绑定，授权码正确且系统状态是可信的，才可以拿到密钥，解密磁盘里的数据；其他任何人想访问设备，不能获得密钥，保证存储数据安全

常用技术：Bitlocker（比特锁）

可信软件基

TSB(Trusted Software Base):

  • 可信软件基由可信管理中心统一管理和调度；
  • 硬件设备公司与可信商业软件公司合作，由其提供可信软件基；
  • 可信设备在TPCM只负责实现硬件支持，主要是在安全处理器中实现TPCM模块

TSB由基本信任基、主动监控机制（控制机制，度量机制，判定机制）、可信基础库，支撑机制组成

  • 基本信任基：具有基本的量度能力，对TSB的启动做验证
  • 主动监控机：制监控系统调用，在ERT的支撑下实现对系统调用软件环境的主动量度和控制（ERT: Entity of Root of Trust， 可信根实体）
  • 支撑机制：通过ERT接口调用，为应用提供完整性量度，加解密，可信认证等服务
  • 协作机制：接收可信策略管理中心的策略下发，上次审计结果，与其他计算平合进行可信协作
  • 可信基准库：存储可信基准值，包括驻留基准值（硬盘）和即时基准值（内存）

Mbedtls

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
$ git clone git@github.com:Mbed-TLS/mbedtls.git
$ cd mbedtls
$ git checkout main

$ git submodule update --init
# Or
$ rm -rf framework
$ git clone git@github.com:Mbed-TLS/mbedtls-framework.git
$ mv mbedtls-framework framework
$ cd framework
$ git checkout 750634d

# 编译
$ mkdir build && cd build
$ cmake ..
$ cmake --build . -j32
$ sudo make install

# 测试
$ cd tests
$ ./test_suite_aes.cbc
AES-128-CBC Encrypt NIST KAT #1 ................................... PASS
AES-128-CBC Encrypt NIST KAT #2 ................................... PASS
AES-128-CBC Encrypt NIST KAT #3 ................................... PASS
AES-128-CBC Encrypt NIST KAT #4 ................................... PASS
...
AES-256-CBC Decrypt NIST KAT #12 .................................. PASS

----------------------------------------------------------------------------

PASSED (72 / 72 tests (0 skipped))

AES

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
crypt_and_hash <mode> <input filename> <output filename> <cipher> <mbedtls_md> <key>

   <mode>: 0 = encrypt, 1 = decrypt

  example: crypt_and_hash 0 file file.aes AES-128-CBC SHA1 hex:E76B2413958B00E193

Available ciphers:
  AES-128-ECB
  AES-192-ECB
  ...
  AES-256-XTS
  AES-128-GCM
  AES-192-GCM
  AES-256-GCM
  ...
  AES-256-KWP

Available message digests:
  SHA512
  SHA384
  SHA256
  SHA224
  SHA1
  RIPEMD160
  MD5
  SHA3-224
  SHA3-256
  SHA3-384
  SHA3-512
  • 准备一个txt文本，内容为’Hello World’
  • 使用 AES-256-GCM 加密，SHA256 验证完整性，密钥为 hex:7a30d862c42e74
1
2
3
4
5
$ echo 'Hello World' >> plain.txt
$ crypt_and_hash 0 plain.txt     plain.txt.enc AES-256-GCM SHA256 hex:7a30d862c42e74
$ crypt_and_hash 1 plain.txt.enc plain.txt.dec AES-256-GCM SHA256 hex:7a30d862c42e74
$ cat plain.txt.dec
Hello World

Hash

1
2
3
4
5
$ generic_sum SHA256 plain.txt
d2a84f4b8b650937ec8f73cd8be2c74add5a911ba64df27458ed8229da804a26  plain.txt

$ sha256sum plain.txt
d2a84f4b8b650937ec8f73cd8be2c74add5a911ba64df27458ed8229da804a26  plain.txt

PKey

  • rsa_genkey - 演示如何生成 RSA 密钥对的应用程序
  • rsa_encrypt - 使用 rsa API 的 RSA 加密参考程序
  • rsa_decrypt - 使用 rsa API 的 RSA 解密参考程序
  • ecdsa - ECDSA 程序示例
  • gen_key - 如何生成私钥的示例
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
$ rsa_genkey

  . Seeding the random number generator... ok
  . Generating the RSA key [ 2048-bit ]... ok
  . Exporting the public  key in rsa_pub.txt.... ok
  . Exporting the private key in rsa_priv.txt... ok

$ rsa_encrypt "Hello World"

  . Seeding the random number generator...
  . Reading public key from rsa_pub.txt
  . Generating the RSA encrypted value
  . Done (created "result-enc.txt")

$ rsa_decrypt

  . Seeding the random number generator...
  . Reading private key from rsa_priv.txt
  . Decrypting the encrypted data
  . OK

The decrypted result is: 'Hello World'

ECDH

密钥交换算法简介：RSA算法再一定程度熵解决了密钥配送问题，但也可以用DH密钥协商算法来解决密钥配送问题。DH密钥协商算法时基于离散对数问题。DH（Diffie-Hellman）密钥协商是由 Whitfield Diffie 和 Martin Hellman 提出，该算法允许通讯双方再不安全的信道交换数据，从而协商出一个会话密钥。

  • Diffie-Hellman 密钥交换：基于有限域的离散对数难以计算所实现
  • Alic 给 Bob 一个大质数 P 和生成元 G
  • Alice 和 Bob 各在 1 ~ P-2 的区间内生成一个随机数并保密
  • Alic发送 $G^A mod P$ 给Bob
  • Bob发送 $G^B mod P$ 给Alice
  • Alice 计算 $(G^B mod P)^A mod P$ 作为密钥
  • Bob 计算 $(G^A mod P)^B mod P$ 作为密钥，与 Alice 相同
  • 生成元的计算方法：
    • 设 13 为 P，则任取 G 在 0 - P-1 内，A 在 1 ~ P - 1 的范围内，生成元 $G^A mod P$ 应当与 A 一一对应的关系
    • 例如 2 的 1 次方到 12 次方取 13 的模与 1 - 12 一一对应因此 2 是 13 的生成元

mbedtls\programs\pkey 目录下：

  • dh_client.c ，DH客户端
  • dh_server.c，DH服务器
  • dh_genprime.c，产生DH共享参数，保存在dh_prime.txt
  • rsa_genkey.c，产生RSA密钥对，保存在rsa_priv.txt、rsa_pub.txt

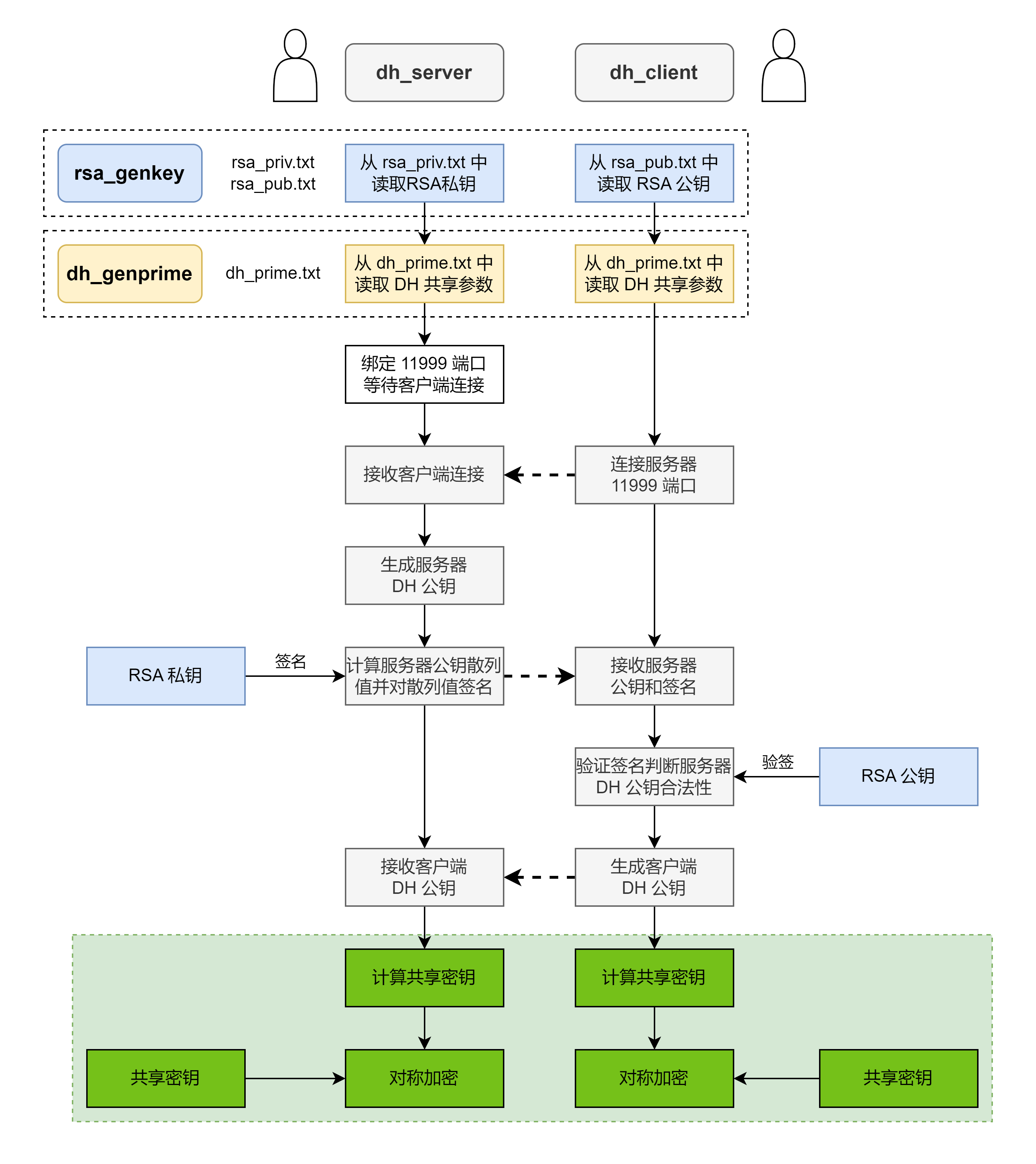
服务器和客户端通过DH密钥协商获得共享密钥

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
$ rsa_genkey

  . Seeding the random number generator... ok
  . Generating the RSA key [ 2048-bit ]... ok
  . Exporting the public  key in rsa_pub.txt.... ok
  . Exporting the private key in rsa_priv.txt... ok

$ dh_genprime bits=2048
  ! Generating large primes may take minutes!

  . Seeding the random number generator... ok
  . Generating the modulus, please wait... ok
  . Verifying that Q = (P-1)/2 is prime... ok
  . Exporting the value in dh_prime.txt... ok

$ cat dh_prime.txt
P = E9D1910FAD096EA00EDB6A6FCADF53DC51D49E775CBC333F04F530343CBB37048804A11925DE5F320F5208D35FC25F076ADBB26730CEC6FCF5F91E325821B098F5F901ABFA51BBD2B8CA4C412820D9AD75BC3668CF71B71CE3643A05D82AC7182657831774DCF1893DB218BE7893332EF4EEAF7DDA353C88CFB6E735B71A83DC0C4182E65082062BFFE70E5C8791EEF8E081BA0187D06F2C67FFE931C5BF6765ECC9A647CA5F36BFA554B1C6589CE84C5F48E610CD96DD4D7AD594D63B0E49984AA22C4EB38655AB0112751C3A49C87D8CD6710BB444C04642394CAB863C78D8CFA50C5494F74BC601D08051FE74313CE986BB3520B34F48986DABF9CF8D9B77
G = 04

$ ./dh_server

  . Seeding the random number generator
  . Reading private key from rsa_priv.txt
  . Reading DH parameters from dh_prime.txt
  . Waiting for a remote connection
  # Once client starts
  . Sending the server's DH parameters                   # 发送服务器的交换参数，这里签了名
  . Receiving the client's public value
  . Shared secret: 7517f59890db14837d888c258d65969c...   # 计算交换共享密钥
  . Encrypting and sending the ciphertext

$ ./dh_client

  . Seeding the random number generator
  . Reading public key from rsa_pub.txt
  . Connecting to tcp/localhost/11999
  . Receiving the server's DH parameters
  . Verifying the server's RSA signature                 # 接收时先验签
  . Sending own public value to server
  . Shared secret: 7517f59890db14837d888c258d65969c...   # 计算交换共享密钥
  . Receiving and decrypting the ciphertext
  . Plaintext is "==Hello there!=="

SM4 国密算法

参考：

1
2
3
4
5
6
7
8
9
10
11
12
13
$ git clone git@github.com:Low-power/mbedtls.git
$ cd mbedtls
$ git checkout mbedtls-2.7-sm4
$ mkdir build && cd build
$ cmake ..
$ cmake --build . -j32
$ cd tests
$ ./test_suite_sm4
SM4 Encrypt_ECB #1 ................................................ PASS
...
SM4 Decrypt_CTR #2 ................................................ PASS

----------------------------------------------------------------------------

代码：

  • 源码：library/sm4.c
  • 头文件：build/include/mbedtls/sm4.h
  • 测试代码：tests/suites/test_suite_sm4.function
  • 测试数据：tests/suites/test_suite_sm4.data
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
/**
 * \brief SM4 context structure
 */

typedef struct
{
    uint32_t rk[32];        /*!<  SM4 round keys    */
}
mbedtls_sm4_context;

/**
 * \brief          Initialize SM4 context
 *
 * \param ctx      SM4 context to be initialized
 */

void mbedtls_sm4_init( mbedtls_sm4_context *ctx );

/**
 * \brief          Clear SM4 context
 *
 * \param ctx      SM4 context to be cleared
 */
void mbedtls_sm4_free( mbedtls_sm4_context *ctx );

/**
 * \brief          SM4 key schedule (encryption)
 *
 * \param ctx      SM4 context to be initialized
 * \param key      encryption key
 * \param keybits  must be 128, 192 or 256
 *
 * \return         0 if successful, or MBEDTLS_ERR_SM4_INVALID_KEY_LENGTH
 */
int mbedtls_sm4_setkey_enc( mbedtls_sm4_context *ctx,
                                const unsigned char *key,
                                unsigned int keybits );

/**
 * \brief          SM4 key schedule (decryption)
 *
 * \param ctx      SM4 context to be initialized
 * \param key      decryption key
 * \param keybits  must be 128, 192 or 256
 *
 * \return         0 if successful, or MBEDTLS_ERR_SM4_INVALID_KEY_LENGTH
 */
int mbedtls_sm4_setkey_dec( mbedtls_sm4_context *ctx,
                                const unsigned char *key,
                                unsigned int keybits );

/**
 * \brief          SM4-ECB block encryption/decryption
 *
 * \param ctx      SM4 context
 * \param mode     MBEDTLS_SM4_ENCRYPT or MBEDTLS_SM4_DECRYPT
 * \param input    16-byte input block
 * \param output   16-byte output block
 *
 * \return         0 if successful
 */
int mbedtls_sm4_crypt_ecb( mbedtls_sm4_context *ctx,
                    int mode,
                    const unsigned char input[16],
                    unsigned char output[16] );

#if defined(MBEDTLS_CIPHER_MODE_CBC)
/**
 * \brief          SM4-CBC buffer encryption/decryption
 *                 Length should be a multiple of the block
 *                 size (16 bytes)
 *
 * \note           Upon exit, the content of the IV is updated so that you can
 *                 call the function same function again on the following
 *                 block(s) of data and get the same result as if it was
 *                 encrypted in one call. This allows a "streaming" usage.
 *                 If on the other hand you need to retain the contents of the
 *                 IV, you should either save it manually or use the cipher
 *                 module instead.
 *
 * \param ctx      SM4 context
 * \param mode     MBEDTLS_SM4_ENCRYPT or MBEDTLS_SM4_DECRYPT
 * \param length   length of the input data
 * \param iv       initialization vector (updated after use)
 * \param input    buffer holding the input data
 * \param output   buffer holding the output data
 *
 * \return         0 if successful, or
 *                 MBEDTLS_ERR_SM4_INVALID_INPUT_LENGTH
 */
int mbedtls_sm4_crypt_cbc( mbedtls_sm4_context *ctx,
                    int mode,
                    size_t length,
                    unsigned char iv[16],
                    const unsigned char *input,
                    unsigned char *output );
#endif /* MBEDTLS_CIPHER_MODE_CBC */


#if defined(MBEDTLS_CIPHER_MODE_CTR)
/**
 * \brief               SM4-CTR buffer encryption/decryption
 *
 * Warning: You have to keep the maximum use of your counter in mind!
 *
 * Note: Due to the nature of CTR you should use the same key schedule for
 * both encryption and decryption. So a context initialized with
 * mbedtls_sm4_setkey_enc() for both MBEDTLS_SM4_ENCRYPT and MBEDTLS_SM4_DECRYPT.
 *
 * \param ctx           SM4 context
 * \param length        The length of the data
 * \param nc_off        The offset in the current stream_block (for resuming
 *                      within current cipher stream). The offset pointer to
 *                      should be 0 at the start of a stream.
 * \param nonce_counter The 128-bit nonce and counter.
 * \param stream_block  The saved stream-block for resuming. Is overwritten
 *                      by the function.
 * \param input         The input data stream
 * \param output        The output data stream
 *
 * \return         0 if successful
 */
int mbedtls_sm4_crypt_ctr( mbedtls_sm4_context *ctx,
                       size_t length,
                       size_t *nc_off,
                       unsigned char nonce_counter[16],
                       unsigned char stream_block[16],
                       const unsigned char *input,
                       unsigned char *output );
#endif /* MBEDTLS_CIPHER_MODE_CTR */
1
2
3
4
5
$ echo 'Hello World' >> plain.txt
$ crypt_and_hash 0 plain.txt     plain.txt.enc SM4-128-CBC SHA256 hex:0123456789abcdeffedcba9876543210
$ crypt_and_hash 1 plain.txt.enc plain.txt.dec SM4-128-CBC SHA256 hex:0123456789abcdeffedcba9876543210
$ cat plain.txt.dec
Hello World

OpenSSL SM2 密钥交换协议